204. Count Primes

Total Accepted: 54299
Total Submissions: 230350
Difficulty: Easy

Description:
Count the number of prime numbers less than a non-negative number, _n_.

Credits:
Special thanks to @mithmatt for adding this problem and creating all test cases.

Hint:

Let’s start with a isPrime function. To determine if a number is prime, we need to check if it is not divisible by any number less than _n_. The runtime complexity of isPrime function would be O(_n_) and hence counting the total prime numbers up to _n_ would be O(_n_²). Could we do better?
As we know the number must not be divisible by any number > _n_ / 2, we can immediately cut the total iterations half by dividing only up to _n_ / 2. Could we still do better?

Let’s write down all of 12’s factors:

As you can see, calculations of 4 × 3 and 6 × 2 are not necessary. Therefore, we only need to consider factors up to √_n_ because, if _n_ is divisible by some number _p_, then _n_ = _p_ × _q_ and since _p_ ≤ _q_, we could derive that _p_ ≤ √_n_. Our total runtime has now improved to O(_n_^1.5), which is slightly better. Is there a faster approach?

public int countPrimes(int n) {
   int count = 0;
   for (int i = 1; i < n; i++) {
      if (isPrime(i)) count++;
   }
   return count;
}

private boolean isPrime(int num) {
   if (num <= 1) return false;
   // Loop's ending condition is i * i <= num instead of i <= sqrt(num)
   // to avoid repeatedly calling an expensive function sqrt().
   for (int i = 2; i * i <= num; i++) {
      if (num % i == 0) return false;
   }
   return true;
}

The Sieve of Eratosthenes is one of the most efficient ways to find all prime numbers up to _n_. But don’t let that name scare you, I promise that the concept is surprisingly simple.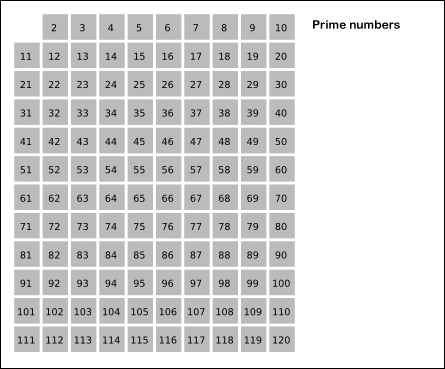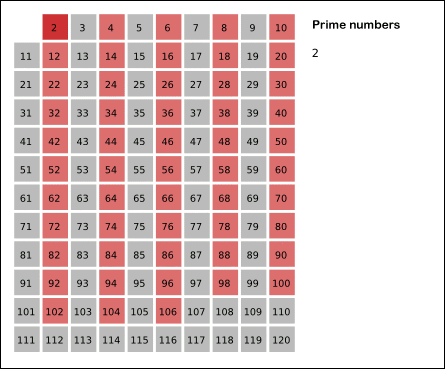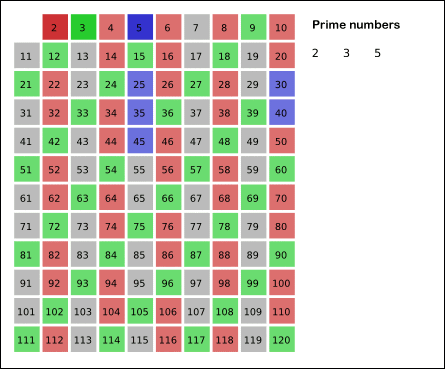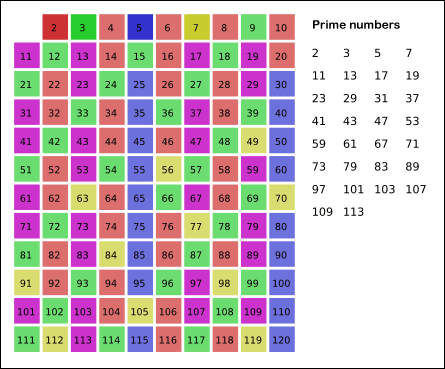Sieve of Eratosthenes: algorithm steps for primes below 121. “Sieve of Eratosthenes Animation” by SKopp is licensed under CC BY 2.0. We start off with a table of _n_ numbers. Let’s look at the first number, 2. We know all multiples of 2 must not be primes, so we mark them off as non-primes. Then we look at the next number, 3. Similarly, all multiples of 3 such as 3 × 2 = 6, 3 × 3 = 9, … must not be primes, so we mark them off as well. Now we look at the next number, 4, which was already marked off. What does this tell you? Should you mark off all multiples of 4 as well?
4 is not a prime because it is divisible by 2, which means all multiples of 4 must also be divisible by 2 and were already marked off. So we can skip 4 immediately and go to the next number, 5. Now, all multiples of 5 such as 5 × 2 = 10, 5 × 3 = 15, 5 × 4 = 20, 5 × 5 = 25, … can be marked off. There is a slight optimization here, we do not need to start from 5 × 2 = 10. Where should we start marking off?
In fact, we can mark off multiples of 5 starting at 5 × 5 = 25, because 5 × 2 = 10 was already marked off by multiple of 2, similarly 5 × 3 = 15 was already marked off by multiple of 3. Therefore, if the current number is _p_, we can always mark off multiples of _p_ starting at _p_², then in increments of _p_: _p_² + _p_, _p_² + 2_p_, … Now what should be the terminating loop condition?
It is easy to say that the terminating loop condition is _p_ < _n_, which is certainly correct but not efficient. Do you still remember Hint #3?

Yes, the terminating loop condition can be _p_ < √_n_, as all non-primes ≥ √_n_ must have already been marked off. When the loop terminates, all the numbers in the table that are non-marked are prime. The Sieve of Eratosthenes uses an extra O(_n_) memory and its runtime complexity is O(_n_ log log _n_). For the more mathematically inclined readers, you can read more about its algorithm complexity on Wikipedia.

public int countPrimes(int n) {
boolean[] isPrime = new boolean[n];
for (int i = 2; i < n; i++) {
  isPrime[i] = true;
}
// Loop's ending condition is i * i < n instead of i < sqrt(n)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i < n; i++) {
  if (!isPrime[i]) continue;
  for (int j = i * i; j < n; j += i) {
     isPrime[j] = false;
  }
}
int count = 0;
for (int i = 2; i < n; i++) {
  if (isPrime[i]) count++;
}
return count;
}

Java:

public class Solution {
    public int countPrimes(int n) {
        if (n < 3)
            return 0;
        int count = n / 2;
        boolean[] isPrime = new boolean[n];
        for (int i = 3; i * i < n; i += 2) {
            if (isPrime[i])
                continue;
            for (int j = i * i; j < n; j += 2 * i) {
                if (!isPrime[j]) {
                    --count;
                    isPrime[j] = true;
                }
            }
        }
        return count;
    }
}

打个小广告

欢迎加入我的小专栏「基你太美」一起学习。