Tri Tiling

In how many ways can you tile a 3xn rectangle with 2x1 dominoes?

Here is a sample tiling of a 3x12 rectangle.

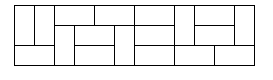
Input

Input consists of several test cases followed by a line containing -1. Each test case is a line containing an integer 0 ≤ n ≤ 30.

Output

For each test case, output one integer number giving the number of possible tilings.

Sample Input

2
8
12
-1

Sample Output

3
153
2131

分析：给你一个3n的框框，用21的框框去填满，问一共有多少种不同的方法。首先，n为奇数肯定是0；当n为偶数时，n=2有3种拼法，当全部都由这三种组成的话f[n]=f[n-2]3;当出现上图两个红圈圈的情况时，我们就又有2（f[n-4]+f[n-6]+……f[0])，所以f(n)=3f(n-2)+2f(n-4)+…+2f(0)，可以解出f(n)=4f(n-2)-f(n-4)，其中f(0)=1,f(2)=3;

ac代码:

#include<iostream>
#include<stdio.h>
#include<algorithm>
#include<vector>
#include<cctype>
#include<cmath>
#include<cstring>
#include<string>
using namespace std;
void solve();
int main()
{
    solve();
    return 0;
}
void solve()
{   
    int n,f[31] = {1,0,3};
    for (int i = 4;i <= 30;i ++)
        f[i] = f[i - 2]*4 - f[i - 4];
    while (scanf ("%d",&amp;n)&amp;&amp;n != -1)
        printf ("%d\n",f[n]);
}

打个小广告

欢迎加入我的小专栏「基你太美」一起学习。