Prim&Dijkstra

发表于 | 分类于 | 阅读次数:

先是求最小生成树的Prim算法

首先输入两个整数 n 和 m，表示图中的顶点数和边数。接下来一共 m 行，每行三个整数 a，b，c，表示一条连接 a 和 b 的权重为 c 的带权无向边。程序最终会将最小生成树上所有边权之和输出。

比如输入下面这张图：

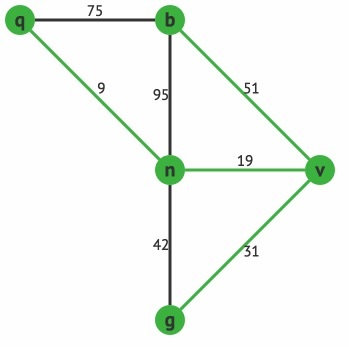
对应的输入数据为

5 7
0 1 75
0 2 9
1 2 95
1 3 51
2 3 19
2 4 42
3 4 31
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#include <iostream>
#include <cstring>
#include <vector>
#include <queue>
using namespace std;

const int INF = 0x3f3f3f3f;

struct Edge {
    int vertex, weight;
};

class Graph {
private:
    int n;
    bool * visited;
    vector<Edge> * edges;
public:
    int * dist;
    Graph (int input_n) {
        n = input_n;
        edges = new vector<Edge>[n];
        dist = new int[n];
        visited = new bool[n];
        memset(visited, false, n * sizeof(bool));
        memset(dist, 0x3f, n * sizeof(int));
    }
    ~Graph() {
        delete[] dist;
        delete[] visited;
        delete[] edges;
    }
    void insert(int x, int y, int weight) {
        edges[x].push_back(Edge{y, weight});
        edges[y].push_back(Edge{x, weight});
    }
    int prim(int v) {
        int total_weight=0;
        dist[v]=0;
        for(int i=0;i<n;++i){
            int min_dist=INF,min_vertex;
            for(int j=0;j<n;++j){
                if(!visited[j]&&dist[j]<min_dist){
                    min_dist=dist[j];
                    min_vertex=j;
                }
            }
            total_weight+=min_dist;
            visited[min_vertex]=1;
            for(Edge &j:edges[min_vertex]){
                if(!visited[j.vertex]&&j.weight<dist[j.vertex]){
                    dist[j.vertex]=j.weight;
                }
            }
        }        
        return total_weight;
    }
};

int main() {
    int n, m;
    cin >> n >> m;
    Graph g(n);
    for (int i = 0; i < m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        g.insert(a, b, c);
    }
    cout << g.prim(0) << endl;
    return 0;
}

再是计算最短路径的Dijkstra算法，Dijkstra 算法和前面的 Prim 算法很相像，都是从一个点开始，每次确定一个点并完成更新，重复操作直至 n 个点都确定为止。

需要注意的是，Dijkstra 不适用于有边权为负数的情况哦，否则会影响算法的正确性。

如果对 Prim 算法的代码还有印象的话，应该可以感觉到，Prim 算法和 Dijkstra 算法极为相似。都会用到一个 visited 数组标记是否已经完成计算，以及一个 dist 数组表示最短路径。不过在 Dijkstra 算法中，dist 存储的就不是到生成树的距离了，而是从源点出发到每个顶点的最短路径。

首先输入两个整数 n 和 m，表示图中的顶点数和边数。接下来一共 m 行，每行三个整数 a，b，c，表示一条连接 a 和 b 的权重为 c 的带权无向边。程序最终会输出从源点出发到所有顶点的最短路径长度。

比如输入下面这张图：

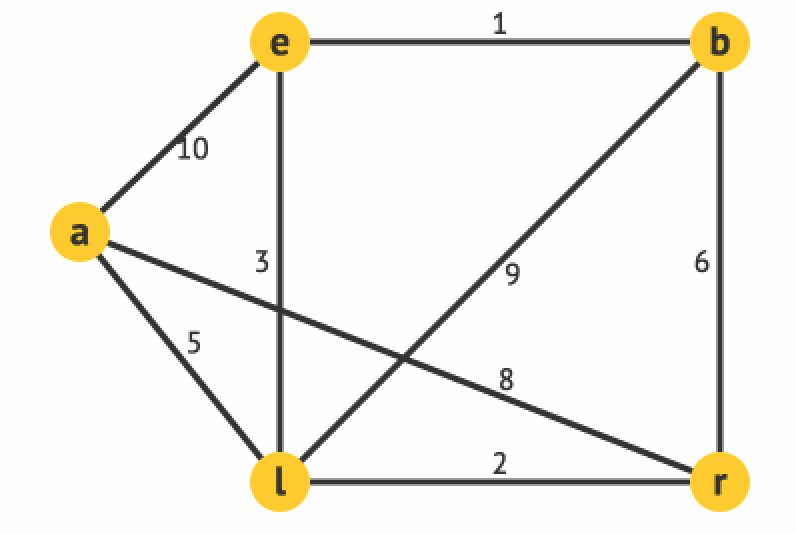
对应的输入数据为

5 8
0 1 10
0 2 5
1 2 3
1 3 1
2 3 9
2 4 2
3 4 6
0 4 8
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#include <iostream>
#include <cstring>
#include <vector>
#include <queue>
using namespace std;

const int INF = 0x3f3f3f3f;

struct Edge {
    int vertex, weight;
};

class Graph {
private:
    int n;
    vector<Edge> * edges;
    bool * visited;
public:
    int * dist;
    Graph (int input_n) {
        n = input_n;
        edges = new vector<Edge>[n];
        dist = new int[n];
        visited = new bool[n];
        memset(visited, 0, n);
        memset(dist, 0x3f, n * sizeof(int));
    }
    ~Graph() {
        delete[] dist;
        delete[] edges;
        delete[] visited;
    }
    void insert(int x, int y, int weight) {
        edges[x].push_back(Edge{y, weight});
        edges[y].push_back(Edge{x, weight});
    }
    void dijkstra(int v) {
        dist[v]=0;
        for(int i=0;i<n;++i){
            int min_dist=INF,min_vertex;
            for(int j=0;j<n;++j){
                if(!visited[j]&&dist[j]<min_dist){
                    min_dist=dist[j];
                    min_vertex=j;
                }
            }
            visited[min_vertex]=1;
            for(Edge &j:edges[min_vertex]){
                if(min_dist+j.weight<dist[j.vertex]){
                    dist[j.vertex]=min_dist+j.weight;
                }
            }
        }
    }
};

int main() {
    int n, m;
    cin >> n >> m;
    Graph g(n);
    for (int i = 0; i < m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        g.insert(a, b, c);
    }
    g.dijkstra(0);
    for (int i = 0; i < n; i++) {
        cout << i << ": " << g.dist[i] << endl;
    }
    return 0;
}

打个小广告

欢迎加入我的小专栏「基你太美」一起学习。