发表于 | 分类于 | 阅读次数:

堆实际上是一颗二叉树，对于大根堆来说，它的特点就是父节点的值大于所有子节点的值。

C++的STL中priority_queue已经帮我们实现好了堆的数据结构，接下来我们一起学习并实践如何实现一个堆并用堆进行排序。

priority_queue是STL的queue这个头文件中定义的数据结构，因此需要额外引用它，即#include <queue>。

阅读全文 »

发表于 | 分类于 | 阅读次数:

蒜头最近在沉迷小说，尤其是人物关系复杂的言情小说。它看到的人物关系描述得很的麻烦的时候觉得非常蒜疼，尤其是人物关系里有冗余的时候。什么是冗余关系呢？

这篇小说里有n句描述人物关系的句子，描述了n个人的关系。

每条句子的定义是这样的：

X<->Y 它的意思是：X认识Y，Y也认识X

我们认为小说中的人物关系是具有传递性的，假如A认识B，B认识C，则A也认识C。

冗余关系的定义：就是即使没有这条人物关系，原来的人物之间的所有关系也照样成立。

比如：

小说中已经提到了A认识B，B也认识C。在此之后再讲A认识C就是一个冗余的关系。

小蒜头想求出一共有多少条冗余关系，你能帮帮它吗？也许并查集能帮上忙哦。

阅读全文 »

发表于 | 分类于 | 阅读次数:

并查集是一个多棵树的数据结构(森林)，每个节点记录一个father[i]表示它的父节点。并查集可以解决集合的合并和查询操作。

阅读全文 »

发表于 | 分类于 | 阅读次数:

最长上升子序列 (Longest Increasing Subsequence, 常简称为 LIS) 是动态规划解决的一个经典问题。

我们先讲一下子序列是什么。一个数组的子序列就是从里面选出一些元素，并将他们保持原有的先后顺序排列。比如[1, 2, 3, 4, 5]的子序列有[1, 3, 5]、[3, 4]，而[1, 5, 3]则不是这个数组的子序列。

这里多介绍一下，还有一个容易与子序列混淆的概念：子串。子串是指从一个数组中选出连续的一个或多个元素，并且保持他们原有的顺序。子串一定是子序列，比如前面的子序列[3, 4]就是子串，但[1, 3, 5]不是子串，因为这三个元素在原数组中并不是连续的。

一句话总结他们的区别，就是子序列可以不连续，而子串必须连续。

上升子序列是指子序列Ai中满足 A1 < A2 < … < An，也就是后面的元素一定比前面的元素大，比如(1, 3, 5)是上升子序列，(1, 3, 3)和(1, 4, 3)都不是。现在来跟我一起解决最长上升子序列的问题吧！(o・・o)/

阅读全文 »

发表于 | 分类于 | 阅读次数:

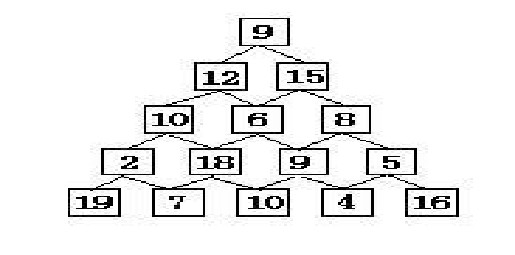
上面这张图是一个数塔问题的例子。每次从顶部元素，就是上图中的9出发，每次可以走到下面相邻的两个节点，比如从9往下相邻的是12和15，6往下相邻的是18和9。找到一条从顶部到底部的路径，使得路径上的数值和最大。

一个直观的贪心策略是每次向下走都选择较大的那一个，得到的一个解是9+15+8+9+10=51，然而我们发现最优的解是9+12+10+18+10=59，也就是说这道题并不适合贪心策略。

接下来我们把问题分解，假如知道从顶点到每个点的最优解的话，最终答案也就能够得出了。假设第i行第j个元素为止的最优解为f[i][j]，可以想到f[i][j]只和f[i-1][j]和f[i-1]j-1有关。也就是说第i行的解只会跟第i-1行的一个或两个元素有关。

阅读全文 »

发表于 | 分类于 | 阅读次数: 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <cstdio>
#include <iostream>
using namespace std;
void quick_sort(int dat[], int l, int r) {
    // 首先请填写下面三个变量的初值
    int i = l, j =r , mid = dat[r];
    do {
        while (dat[i] < mid) ++i;
        while (dat[j] > mid) --j;
        if (i <= j) {
            swap(dat[i], dat[j]);
            ++i; --j;
        }
    } while (i < j);
    // 接下来请填写第一个递归调用的参数，仔细回顾一下刚刚讲的快速排序算法的思想哈。
    if (l < j) quick_sort(dat,l,j);
    // 接下来请填写第二个递归调用的参数。
    if (i < r) quick_sort(dat,i,r);
}
int main() {
    int dat[10] = {1, 4, 3, 2, 5, 3, 2, 5, 10, 9};
    quick_sort(dat, 0, 9);
    for (int i = 0; i < 10; ++i)
        printf("%d ", dat[i]);
    return 0;
}

发表于 | 分类于 | 阅读次数: 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
#include<iostream>
using namespace std;
class Node {
public:
    int data;
    Node* next;
    Node(int _data) {
        data = _data;
        next = NULL;
    }
};
class LinkList {
private:
    Node* head;
public:
    LinkList() {
        head = NULL;
    }
    void insert(Node *node, int index) {
        if (head == NULL) {
            head = node;
            return;
        }
        if (index == 0) {
            node->next = head;
            head = node;
            return;
        }
        Node *current_node = head;
        int count = 0;
        while (current_node->next != NULL && count < index - 1) {
            current_node = current_node->next;
            count++;
        }
        if (count == index - 1) {
            node->next = current_node->next;
            current_node->next = node;
        }
    }
    void output() {
        if (head == NULL) {
            return;
        }
        Node *current_node = head;
        while (current_node != NULL) {
            cout << current_node->data << " ";
            current_node = current_node->next;
        }
        cout << endl;
    }
    void delete_node(int index) {
        if (head == NULL) {
            return;
        }
        Node *current_node = head;
        int count = 0;
        if (index == 0) {
            head = head->next;
            delete current_node;
            return;
        }
        while (current_node->next != NULL && count < index -1) {
            current_node = current_node->next;
            count++;
        }
        if (count == index - 1 && current_node->next != NULL) {
            Node *delete_node = current_node->next;
            current_node->next = delete_node->next;
            delete delete_node;
        }
    }
    void reverse(){
        if(head==NULL){
            return;
        }
        Node *next_node,*current_node;
        current_node=head->next;
        head->next=NULL;
        while(current_node!=NULL){
            next_node=current_node->next;
            current_node->next=head;
            head=current_node;
            current_node=next_node;
        }
    }

};
int main() {
    LinkList linklist;
    for (int i = 1; i <= 10; i++) {
        Node *node = new Node(i);
        linklist.insert(node, i - 1);
    }
    linklist.output();
    linklist.delete_node(3);
    linklist.output();
    linklist.reverse();
    linklist.output();
    return 0;
}

发表于 | 分类于 ， | 阅读次数:

Given a sequence of K integers { N1, N2, …, NK }. A continuous subsequence is defined to be { Ni, Ni+1, …, Nj } where 1 <= i <= j <= K. The Maximum Subsequence is the continuous subsequence which has the largest sum of its elements. For example, given sequence { -2, 11, -4, 13, -5, -2 }, its maximum subsequence is { 11, -4, 13 } with the largest sum being 20.

Now you are supposed to find the largest sum, together with the first and the last numbers of the maximum subsequence.

阅读全文 »

发表于 | 分类于 ， | 阅读次数:

At the beginning of every day, the first person who signs in the computer room will unlock the door, and the last one who signs out will lock the door. Given the records of signing in’s and out’s, you are supposed to find the ones who have unlocked and locked the door on that day.

阅读全文 »