问题描述
有n个格子,从左到右放成一排,编号为1-n。
共有m次操作,有3种操作类型:
1.修改一个格子的权值,
2.求连续一段格子权值和,
3.求连续一段格子的最大值。
对于每个2、3操作输出你所求出的结果。
select * from utils
Donald wishes to send a gift to his new nephew, Fooey. Donald is a bit of a traditionalist, so he has chosen to send a set of N classic baby blocks. Each block is a cube, 1 inch by 1 inch by 1 inch. Donald wants to stack the blocks together into a rectangular solid and wrap them all up in brown paper for shipping. How much brown paper does Donald need?
Each employee of a bureaucracy has a job description - a few paragraphs that describe the responsibilities of the job. The employee’s job description, combined with other factors, such as seniority, is used to determine his or her salary.
The Hay Point system frees the Human Resources department from having to make an intelligent judgement as to the value of the employee; the job description is merely scanned for words and phrases that indicate responsibility. In particular, job descriptions that indicate control over a large budget or management over a large number of people yield high Hay Point scores.
You are to implement a simplified Hay Point system. You will be given a Hay Point dictionary and a number of job descriptions. For each job description you are to compute the salary associated with the job, according to the system.
Despite YY’s so much homework, she would like to take some time to play with her minions first.
YY lines her minions up to an N*M matrix. Every minion has two statuses: awake or asleep. We use 0(the digit) to represent that it is asleep, and 1 for awake. Also, we define the minions who are around a minion closest in one of the eight directions its neighbors. And every minute every minion will change its status by the following specific rules:
If this minion is awake, and the number of its neighbors who are awake is less than 2, this minion will feel lonely and turn to asleep.
If this minion is awake, and the number of its neighbors who are awake is more than 3, this minion will turn to asleep for it will feel too crowded.
If this minion is awake, and the number of its neighbors who are awake is exactly 2 or 3, this minion will keep being awake and feel very happy.
If this minion is asleep, and the number of its neighbors who are awake is exactly 3, this minion will wake up because of the noise.
Note that all changes take place at the same time at the beginning of a specific minute.
Also, some minions will get bored and leave this silly game. We use ‘X’s to describe them. We suppose that a minion would leave after T minutes. It will leave at the end of the Tth minute. Its status is considered during the change at the beginning of the Tth minute, and should be ignored after that. Of course, one minion will not leave twice!
YY is a girl full of curiosity and wants to know every minion’s status after F minutes. But you know she is weak and lazy! Please help this cute girl to solve this problem :)
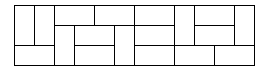
In how many ways can you tile a 3xn rectangle with 2x1 dominoes?
Here is a sample tiling of a 3x12 rectangle.
A tug of war is to be arranged at the local office picnic. For the tug of war, the picnickers must be divided into two teams. Each person must be on one team or the other; the number of people on the two teams must not differ by more than 1; the total weight of the people on each team should be as nearly equal as possible.
The first line of input contains n the number of people at the picnic. n lines follow. The first line gives the weight of person 1; the second the weight of person 2; and so on. Each weight is an integer between 1 and 450. There are at most 100 people at the picnic.
Your output will be a single line containing 2 numbers: the total weight of the people on one team, and the total weight of the people on the other team. If these numbers differ, give the lesser first.